머리말
1주차에는 1주차 합격, 선택과목 수강 등 다양한 주제와 함께 담담하게 교수님과 인사를 나누는 시간을 가졌습니다. 사실 인공지능을 공부하는 사람에게 통계학이 필수라는 사실은 아무도 모른다. 머신 러닝을 처음 접하는 사람들은 “통계는 컴퓨터로 어떻게든 분석하지 않나? 공부를 왜 해야 할까요?” 저도 머신러닝 초보지만 모델을 경험하면서 많은 것을 느꼈습니다. 물론 scikit-learn 라이브러리는 기본적인 모델 구조를 제공하지만, 데이터를 잘 다루지 못하는 머신러닝 연구자는 절대 잘 할 수 없다는 생각이 들었습니다. 이런 경험 때문에 확률변수론은 등급 과목이 아니라 나에게 정말 필요한 지식을 습득할 수 있는 기회라는 생각이 들었다.
무작위 실험 지정
(무작위) 실험: 무작위로 선택된 특정 조건에서 불확실한 결과를 초래하는 과정입니다. 쉽게 말하면 같은 조건에서 반복해도 결과는 다른 실험이다.
결과(샘플): 실험 결과입니다.
샘플 공간: S로 표시되는 가능한 결과의 집합입니다.
사건: S의 부분집합
확률의 정의: “이벤트”에 할당된 음수가 아닌 숫자입니다.
우리가 알고 있는 것과는 달리 양수여야 합니다. 1보다 클 수 있습니다. 그러나 이것은 정의에 의해서만 사실이며 나중에 1보다 작거나 같아야 함을 증명할 수 있습니다.
교차는 동시에 두 개 이상의 집합에 포함된 공통 요소 집합을 나타냅니다. 두 집합이 교차하지 않으면 상호 배타적이라고 합니다.
확률의 공리
확률 변수 이론의 다양한 정리를 증명하는 데 필요한 기본 공리를 살펴보겠습니다.
공리 1: 0 ≤ P(A)(≤ 1)
공리 2: P(S) = 1
공리 3: A와 B가 동시에 일어날 수 없는 사건이라면
또는 A와 B가 상호 배타적인 경우
또는 A ∩ B = ∅
P(A ∪ B) = P(A) + P(B)
공리 3′: A1, A2, A3, …가 모든 i≠j에 대해 Ai ∩ Aj = ∅인 일련의 사건인 경우(쌍으로 상호 배타적)
조건부 확률
수능 공부를 하면서 많이 공부했던 조건부 확률에 대한 내용입니다.
예를 보고 이해해 봅시다.
아래 표와 같이 상자에 100개의 저항이 있다고 가정합니다.
현장에서 저항을 선택하면 다음과 같이 세 가지 이벤트가 정의됩니다.
A: 선택한 저항이 47옴인 이벤트
B: 선택된 저항이 5% 공차인 이벤트
C: 선택된 저항이 100옴인 이벤트

상자에서 저항을 선택합니다. 이 저항의 공차는 5%입니다. 이 저항이 47옴일 확률은 얼마입니까?

위의 예를 사용하여 조건부 확률의 정의를 살펴보겠습니다.

조건부 확률 P(A|B)는 표본 공간 S에 대한 확률이 아니라 표본 공간이 B일 때의 확률을 의미합니다.
따라서 다음 식을 유도할 수 있습니다.

총 확률 정리
에스 = B1 ∪ B2 ∪ B3 ∪ … ∪ Bn Bi ∩ Bj = ∅인 경우, i ≠ j(쌍으로 배타적인 경우)
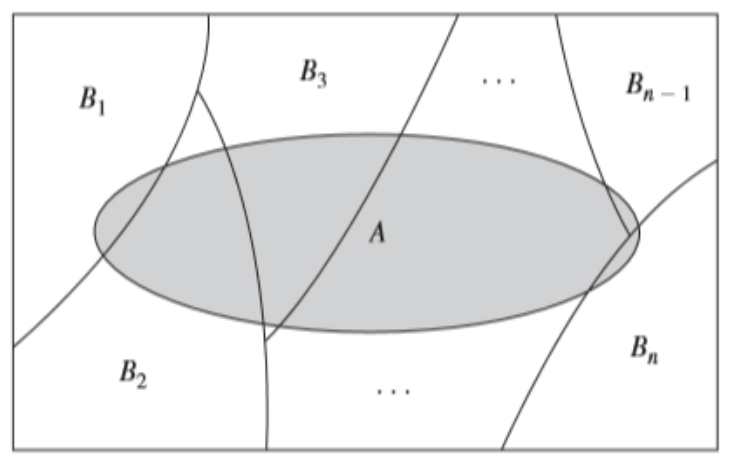
분배 법칙을 사용하여 총 확률에 대한 다음 정리를 얻을 수 있습니다.
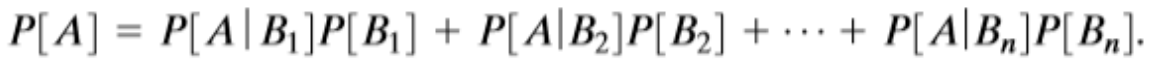
베이즈 규칙

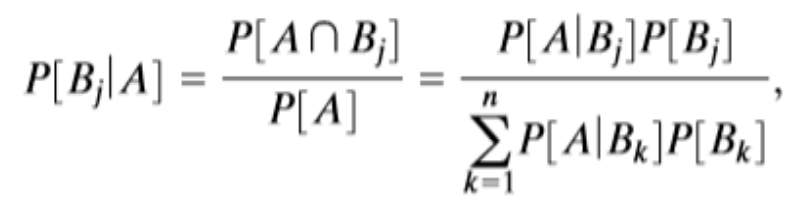
사건으로부터의 독립
통계적 독립성의 정의
두 사건 A와 B는 P(A ∩ B ) = P(A)P(B)인 경우 통계적으로 독립이라고 합니다.
두 사건 A와 B가 통계적으로 독립이면 P(A|B) = P(A) 및 P(B|A) = P(B)입니다.


